我们为什么“视而不见”？论成像与光场的关系|邵晓鹏专栏第三季

执象而求，咫尺千里。——弘一大师

引子

“什么是计算光学？”我相信这个问题几乎是每个做计算成像的人都会遇到，而且问这个问题的人多是大同行甚至是外行的领导，我们该怎么回答呢？如果一本正经地背定义：“计算光学成像是下一代光电成像技术，是光电成像技术步入信息时代的必然产物，其本质是光场信息的获取和解译，是在几何光学成像的基础上有机引入物理光学信息，以信息传递为准则，通过信息获取更高维度的信息……”估计大多数人都会皱起眉头。那么，我们该怎么回答？说计算光学是信息光学，肯定不行；说是对成像后的图像进行数据处理，当然更不行；说是光场成像，不仅有光场相机当年带来的歧义，还得去解释什么是光场，卷入了更为复杂的解释怪圈……

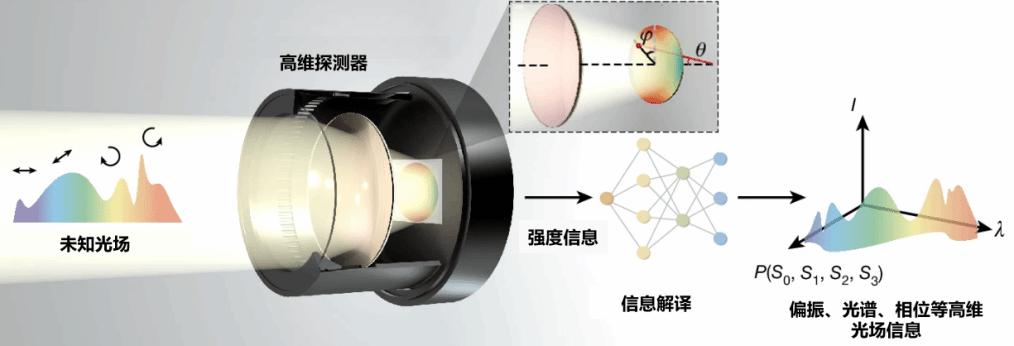
那么，我们该怎么解释呢？

近年来，又有一种流行的说法是“凡物皆可成像”，那么，这个像是什么？“凡物皆可成像”背后的机理到底是什么呢？

要回答这些问题，我们还得去“刨祖坟”。

一、象：虚幻也——物象共轭1、乱象：相、象与像

中文很有意思，相机拍出来的明明是“图像”，我们却习惯性地称之为“相片”；在数字图像刚开始流行时，它的名字是“图象”，而曾几何时，“图象”却又变成了“图像”，真是乱象丛生！年龄小的人，如果看到“图象”一词，第一反应则是写错字了。

其实，这都是文化发展之使然。正如马未都说“历史没有真相，只残存一个道理”一般，想要了解这些差异，只能先从“相”、“象”和“像”汉字出现的时间寻找蛛丝马迹，然后就是“从俗”。不过，这些其实并不重要，就像“阿房宫”的读音从“ē páng gōng”变化到“ā fáng gōng”一样，读错了的人成了大多数，“从俗”规则却让那些读对了少数人开始疑问：为什么学得好的人却屈从了学得差的呢？其实，历史向来如此，没有什么绝对的正确和绝对的错误，放过自己比委屈自己更好。你看看，这里的三个“xiang”字的英语都是“image”，多比对一下不同时期出版的书，“一笑了之”的态度会让你更加释然。

有时候，无知会让人更加自信。如果你把“物象共轭”写成“物像共轭”，估计没有几个人会站出来指指点点，甚至很多人会认为从来就该如此。至于这些是咬文嚼字的事儿，还是让汉语言专家去解决吧，我们关心的是关于成像的事儿。

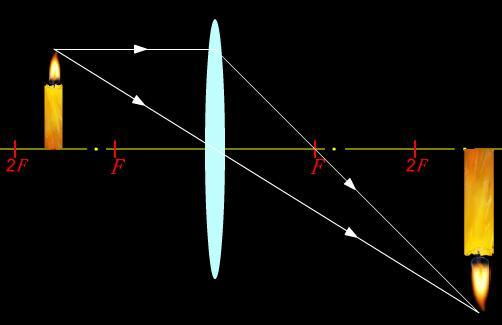
图 透镜成像原理

下面，我们要回答成像中的“像”到底是什么。

2、“像”的真相到底是什么？

从墨子的小孔成像，到后来的透镜成像，再到相机的出现，我们看到的“像”其实都是人的眼睛主观感受到的强度（色彩）信息，这个“像”就是物象共轭的那个“象”，也是物理书上讲的那个实像。

其实，这还没有说到点子上，这个“像”的本质是什么，还需要进一步分析。我们说的实像是能够在胶片和CMOS芯片曝光得到一幅货真价实的图像，而不是镜子和湖面那种“镜花水月”的虚像，也就是说，实像之所以能称之为“实”，是因为它本质上是从物空间到像空间的一种能量重新分布形式，而能被实际探测接收到。显然，这个实像是光场的一种分布形式，而且是能量分布。

再进一步，既然是“像”，那么它必须跟“物”要很像很像，物象共轭的和谐就是如此而来。那么，“很像”意味着什么呢？这里蕴含的其实是实变换，也就是像必须是实数。这就让我们回到了《几何光学》讲述薄透镜成像的案例中，之所以用被称之为“薄透镜”的理想透镜做主角，就是说不考虑任何像差的情况下，几何成像本质就是物到像的实变换，像与物是完全相似的。

然而，任何镜头都存在程度不同的像差，这就意味着成像不再是实变换，而变成了复变换，其幅值的平方即强度就构成了像中的每一个点。于是，为了让像更“像”，在设计光学镜头时就需要付出更多代价，其光学性能虽然只是提升了一点点，带来的成本增加却远远超出预期！

图 光学镜头的像差

3、“像”的场分布

既然任何镜头都有像差，任何成像过程都不满足薄透镜式的无像差模式，那么，所有的像都是复数光场的分布形式。于是，在数学上，我们就可以认为传统成像的光学系统设计过程其实是将像的复数场约束到其能量分布与物的强度实数场分布差异满足最优需求。当然，理想透镜成像的复数场中相位是0。其实，这个过程非常复杂，你瞧：一个“简单”的50mm f/1.4标准摄影镜头系统有大约45个优化变量，你能说它简单吗？当然，这个过程基本上可以交由软件来干，但遇到新的问题是：继续减小体积重量、降低成本，那该怎么办呢？显然，答案是传统光学能够发挥的空间已经不大了。

那么，我们就该回过头来想一想：到底是什么原因把我们给逼上了如此的境地呢？“执象而求，咫尺千里”，我甚至有理由怀疑，弘一大师的这句话就是在告诫我们一味儿执念于“像”这个只有强度（色彩）分布的实数场，已然忘记了光场的多维度特性，尤其是那些我们“视而不见”的信息，也许，它们才是我们开启这扇大门的钥匙。

二、视而不见

王阳明说：“你未看此花时，此花与汝心同归于寂，你来看此花时，则此花颜色一时明白起来。”

那么，我们为什么“视而不见”呢？“视而不见”的原因无非分主观和客观两种。主观上的“视而不见”是因为有“难言之隐”，故意而为之；而客观上的“视而不见”，则是能力上的缺陷，主观上有想法，但无能为力。我们这篇文章里讲的是客观上能力的问题。

有一种说法是人类80%以上的信息获取来自眼睛，可是，我们的眼睛却也存在着局限，比如红外的世界我们看不到，偏振也看不到，准确一点说：我们的眼睛只能感受到380~780 nm可见光这个波段的强度信息，当然，幸运的是人眼有红绿蓝三种锥状细胞，让我们可以看到色彩斑斓(或彩色)的世界。

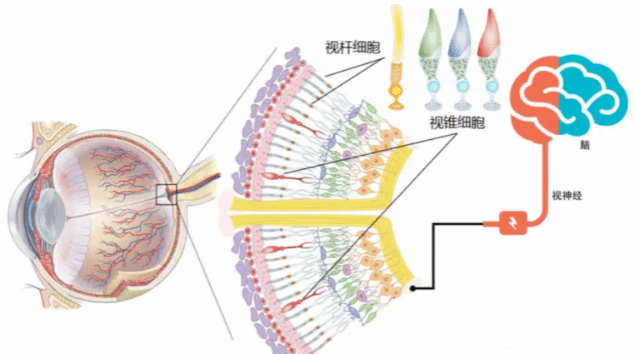
图 人眼视锥细胞的颜色感知

然而，我们从光场的性质来看，人眼能感受到的信息实在太少太少：只有区区可见光波段400 nm谱宽的强度信息！紫外、红外等光谱、偏振信息、相位等等统统“视而不见”！

于是，就有人说：“看不见就看不见呗，眼不见心不烦！再说，你看到这个世界上有哪一个动物能看到全部的你所谓的那个光场信息？”这句话说得似乎很有道理，但是，我们解决的是科学问题，不是人生态度。人眼客观上的“视而不见”，让我们有意无意地把焦点聚在了单一物理量——强度，而且，就连胶片、CCD和CMOS探测器这些感光元件都是参照人眼设计（当然，像光电效应这样的物理规律必须要遵守），这就必然造成了信息的缺失，而恰恰就是因为这些信息的缺失，导致我们不得不付出更多的代价。

三、物象共轭的代价

物象共轭付出代价的原因是过度追求“表相”，也就是像的逼真。一幅照片与原物相似程度越高，看起来就越逼真，这里面当然会牵扯到很多的因素，比如说形变、色差、锐度、饱和度等等，典型的就是摄影镜头的设计，为了“逼真”效果，不得不上设计加工复杂的非球面、昂贵的萤石、甚至多层镀膜衍射元件等各种手段，做出了一个又一个被奉为经典、各种光环加身、死贵死贵的镜头。不信的话，你就玩一玩徕卡之类小众的相机，买个Leica 75mm/F1.25试试。

图 Leica镜头

当然，付出代价的不仅仅是摄影镜头，几乎所有的成像光学系统都是按照物象共轭法则设计，衡量成像品质的原则依然是像的逼真程度，只不过把逼真程度的描述变成了点扩散函数（PSF）此类参数而已。尽管工业界已经把光学成像镜头的价钱做得很便宜了，但是对于航天、航空和无人机载荷的应用来讲，光学系统的要求越来越高，用专业人士的话说其难度已经达到了传统的设计极限，几乎没有办法再优化了；诸如手机类的消费级产品，对摄影镜头的设计要求更是苛刻，不仅要满足大底（1英寸CMOS探测器甚至更大）的需求，而且还面临着镜头减薄、功能更强的挑战，传统的设计方法难以应付。究其原因，还是单一的强度探测惹的祸，毕竟，在光学系统设计上只有一个物理量的约束条件带来的数学问题还是很麻烦，自由度少了，设计难度自然会增加。

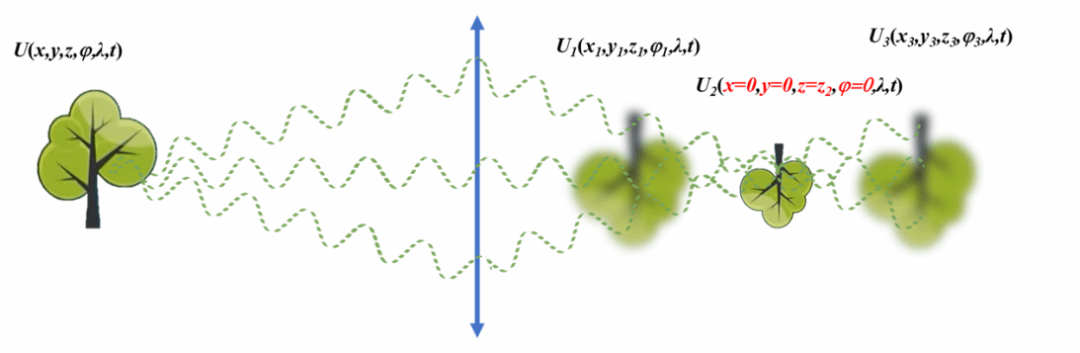
图 传统成像“零”像差约束示意图

同样因为物象共轭带来麻烦的还有自适应光学和合成孔径。大气扰动对成像的影响很严重，自适应光学成了解决该问题的法宝。可是，对于自适应光学系统而言，一般的应用根本用不起，动辄几千万的设备让人望而却步。有没有便宜又好用的自适应光学系统，这是光电成像人的梦想。

这几年，计算光学解决大气自适应的问题研究越来越多，从探测器到人工智能的深度学习处理，在论文疆场上取得一个又一个胜利，于是，就有很多人在摩拳擦掌地想把这些成果应用到实际工作中。更多的人投入到解决光学扰动的问题当然是好事，把更多的坑填上，离应用就不会太远。但如果只关注强度信息，对其他物理信息“视而不见”，这势必会走偏了路。相比起大气扰动，光学合成孔径更是一个大麻烦，至少，在解决大气扰动方面还有招儿，可是光学合成孔径之路之艰难，尤其是迈克尔逊干涉型的分布式合成孔径，更是难中难！其实，其核心问题还是卡在了光场单一物理量约束上，因为在解决这些问题的时候，我们不自觉地就扛起了点扩散函数的旗，可是，你要知道，那在线性约束条件下的产物，其依据依然还是看强度的空间分布情况。

图 干涉仪

那么，该怎么看待庄重严肃的“物象共轭”呢？是追求其极致还是去打破它？该从哪些方面入手呢？

四、绘画未来“视”界的工具：光场

在成像过程中，对焦是个技术活儿，因为只有对好成像物体的焦面，才能成出清晰的像。对焦的方法有很多：测距、相位、爬山、图像处理等等，目的就是要尽可能地“物象共轭”。好，问题来了，那就是对焦要准，严格地讲是对焦精度要高，才能获得清晰的图像，而一旦产生了离焦，图像就会有一定程度的模糊。

图 城市背景离焦模糊现象

注意：我这里讲的是对焦精度高，那就意味着在合焦的一定范围对焦，满足精度都是没问题的。这种问题尤其会发生在景深大的成像过程中，在很宽一段范围内成像都是清晰的，这对拍清晰图像很重要，可是对图像测量可不是好事，因为成像距离不同，带来的物像放大比例也不同，导致误差变大。这种情况，在十多年前我给一个研究所做的图像测量项目中就遇到过，必须要采取额外的方法解决才行。回到对焦的话题，它带来了什么问题？这个问题就是成像往往很难严格合焦，图像大多时候也都是满足人眼视觉效果就可以了，而它本身已经有一点点离焦了，只是这个离焦在我们的容忍范围而已。那么，我们继续扩大离焦范围，你会发现，图像变得越来越模糊，于是就有了很多去模糊的图像处理方法，也有诸如编码曝光解决运动模糊等成像方法，但是，一旦模糊程度变大之后，受到算法的限制，往往效果都不太好。其实，这个问题我在之前的文章里讲过，按照点扩散函数做离焦图像的恢复效果往往都不会很好，因为这里面有点扩散函数过零点的问题存在，不再赘述。

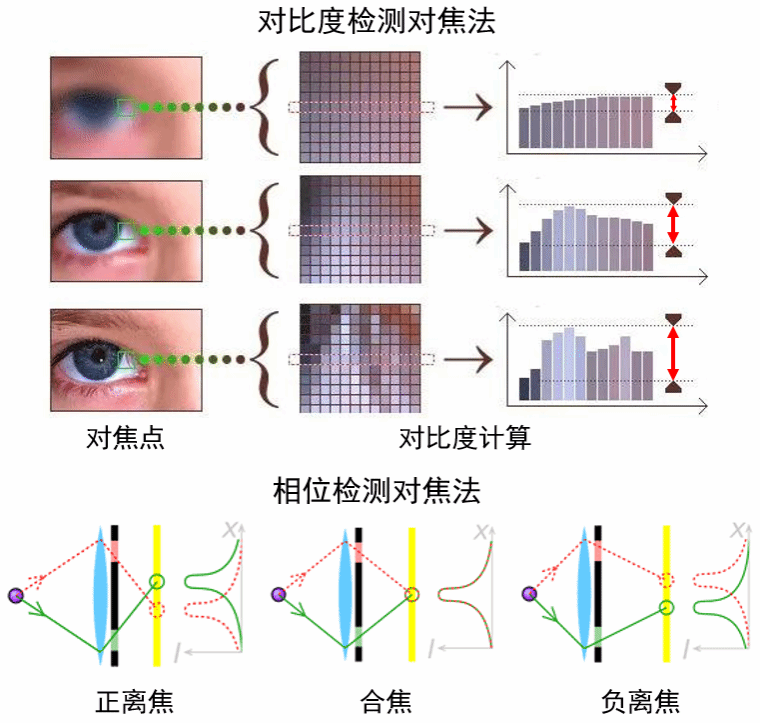
图 对比度检测对焦法与相位检测对焦法

现在，我们抛开上面这些问题，换个角度，回到光场再看这个问题。根据成像光学理论，只要完整精确地获得了像场中的光场信息，理论上，我们就能恢复出图像，而不管离焦与否。

于是，就有人问：如果像你说的这么简单，为什么这么多年很少看到有人去做呢？

首先要说明的是，话简单，但做起来并不简单。原因有二：一是光场获取并不容易，到目前为止，对于多物理量的同时探测依然很困难，因为我们现在的探测器都是基于光电效应，探测到的依然还只是强度信息，对于相位、偏振等等只能设计专门的方法才有可能得到，要得到高精度的光场信息很难；二是算法的局限性，因为受到计算模型和计算精度的限制，目前的图像重建算法即使建立在很准确的模型基础上，因为数字计算的问题，依然会产生较大的偏差，这也就是去运动模糊和离焦复原为什么效果不好的原因，详细内容可以参照“计算光学成像中的数学问题思考”一文。尤其是在计算能力很有限的年代，即使再聪明的学者，也难去闯光场信息恢复这条荆棘之路。所以，并不是前辈们不聪明，而是没有好的计算条件而已。

然后，我们还是回到光场来分析成像的过程，携带着物面信息的光透过透镜后，当经过焦点后投影在像面上时，我们看到的是强度的空间分布，当然，这里肯定有像差，像差可以由圆域正交分解的Zernike多项式进行量化计算，Zernike多项式的每一项与成像镜头不“理想”所引起的几何像差多项式对应，Zernike多项式可以方便的分析成像系统中不同像差的程度。现有的光学系统设计往往会按照要求把像差控制到最优，这个像场主要是光强幅值的分布，而相位往往趋近于0，所以看起来物象共轭了；当在镜头后取非合焦像面的任一光场面时，我们看到的图像将不再是熟悉的物象共轭形式上的像了，而是光场幅值看起来模糊的像，这个像虽不再熟悉，但如果知道光场的相位信息，那么，我们就能恢复出一幅看起来比较“nice”的像，当然，像质取决于图像恢复算法。

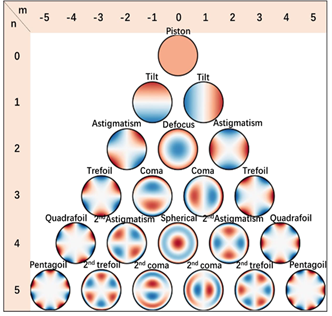
图 Zernike多项式前21项对应的像差含义

于是，我们就有理由相信：携带了物信息的光场，经过任何介质，无论是透射还是反射，只要有办法获取到良好的光场信息（所谓良好就是具有较好信噪比），光场恢复算法都能解译出物的像，这就是“万物皆可成像”的解释。

五、其实还是维度问题

那么，以光场为核心的成像方法都能带来哪些好处呢？

首先是光学系统设计的问题。光学系统从球面设计到非球面设计，从非球面到自由曲面，经历了一个又一个发展阶段，光学系统从很复杂变得相对简单，但是，因为其设计准则还是依据以光强为约束的点扩散函数理论，从光场物理量上看还仅仅只有光强这一个约束参数，成像也依然是严格的物象共轭方式，所以，我们认为这些方法还是停留在像差约束阶段，属于典型的传统光学系统设计方法，并没有跳出线性的窠臼。

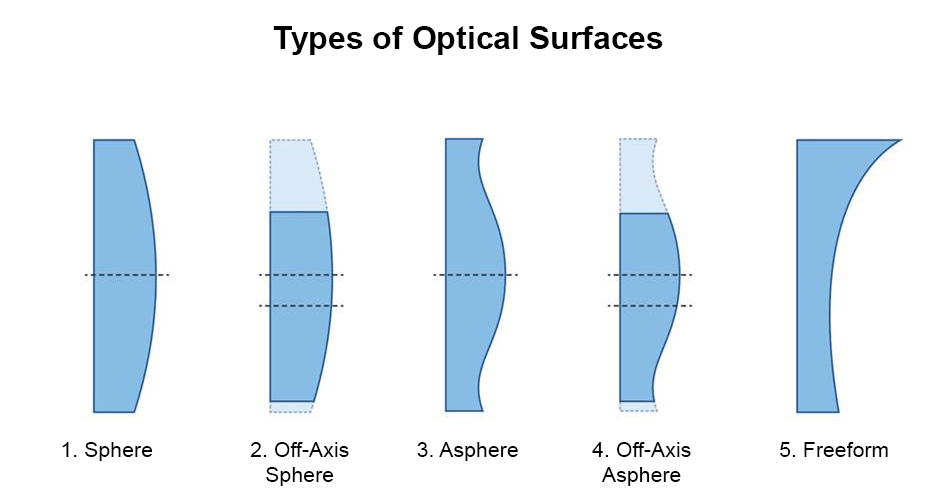
如果采用了以多维度光场为核心的成像方法，对于光学系统设计而言，其实我们只需要知道相位信息即可。如果有了相位信息，从理论上，我们就可以很好地恢复出图像，原理跟自适应光学相类似。问题就变得简单多了。原先我们辛辛苦苦磨镜子，打磨得面型精度要达到至少λ/20，装配对精度的要求更加严格，然后还要保持镜子“不变形”，需要采取各种支撑结构调整镜面；而一旦离焦了，原因还要分析一大堆，能不能采取措施，能解决到什么程度还都不好说。现在有了带相位的光场信息之后，剩下的问题交由算法来解决。

图 望远镜主镜加工

然后是光学合成孔径的难题。之前我在《“破镜重圆”——光学合成孔径》一文中讲过：“破镜重圆”真的很难，究其原因就是单一物理量光强的约束特性，而合成孔径能实现的条件就是要有步调一致的相位。换个角度思考问题，如果采用光场记录结果，相当于每个子镜都有自己的光场分布信息，做好光场的拼接工作，下面的问题就是在时间维和空间维上通过算法让相位步调尽可能一致，达到合成孔径的目的。其实，在这里有强度和相位两个物理量在同时做约束，从数学上做多个场的时空统一规范，在算法上突破合成孔径的难题，这才是我们下一步努力的目标。

其实，现有的光学成像中还存在大量的问题，很多都是卡在维度上，尤其是按照常规的强度维来约束解决问题，导致的结果是一头简单了，另外一头就会变得复杂。那么，平衡一下，在设计成像范式的过程中，改变测量，把难度前移一下，以多维度光场来替代单一强度物理量的约束，放宽约束条件，改成以光场信息解译的问题，问题就会变得简单。

六、无处逃避，不得不见

是不是只要掌握了光场获取和解译的方法，我们就能轻易举起绘画未来“视”界这杆大旗呢？怎么才能同时获取光强和相位等信息呢？

在之前的文章中，我多次强调过，信息不会无中生有，计算成像的引擎是升维。目前，对于超出强度之外的光场信息获取问题，依然还比较复杂，但有路可走。

之前，我们因为受到传统的惯性和算力的限制，在超出强度之外的光场信息做的工作很少，而计算光学成像的灵魂是光场，如果以强度代替光场的以偏概全模式，必然缺失了其他维度的信息，光场的解译便带来很大困难。

现在，我们走到了光学成像发展的关键隘口，已无处逃避；原先“视而不见”的态度，也必须转变，那就是“不得不见”。

不能逃避的问题有多维光学信息获取的问题和算法的问题。在这里，我简单介绍一下相位获取的方法。获取相位的方式可以简单划分为两类：系统测量以及计算恢复。

前者主要包括干涉测量以及非干涉测量，其中干涉测量通常利用信号光与参考光之间产生的干涉条纹来直接提取相位，而非干涉测量通常为单臂结构，代表性器件为波前传感器，其工作原理是通过分析参考图像与信号图像之间的差异定量提取相位梯度信息，进而结合二维梯度积分算法获得相位信息。波前传感器目前的空间分辨率不仅可以满足光学像差的测量，也能够用于定量相位成像。

相较于系统测量，基于计算恢复的方法通常在光学系统复杂度方面更具优势，可以分为迭代型和非迭代型相位恢复算法，前者通过优化算法结合先验信息恢复相位信息，代表性方法包括交替投影相位恢复算法、相位多样性等等。这类方法的收敛性一般是非确定性的，额外的先验信息（如：目标稀疏性等）有助于算法收敛。非迭代型相位恢复算法则可以通过数值求解的方式直接获取相位信息，比如：强度传输方程等。算法主要面临的是非线性和数字计算的问题，我们需要寻求更佳的数学模型和重建信噪比高的方法，好在现在有了人工智能，它在解决复杂的非线性问题上有卓越的表现，在低信噪比的处理上表现也不俗，这些工具都值得我们去好好开发。我们现在正在致力于多维探测器的设计工作，其中就包含相位感知的探测器，一旦推广起来，应用起来就变得简单多了。

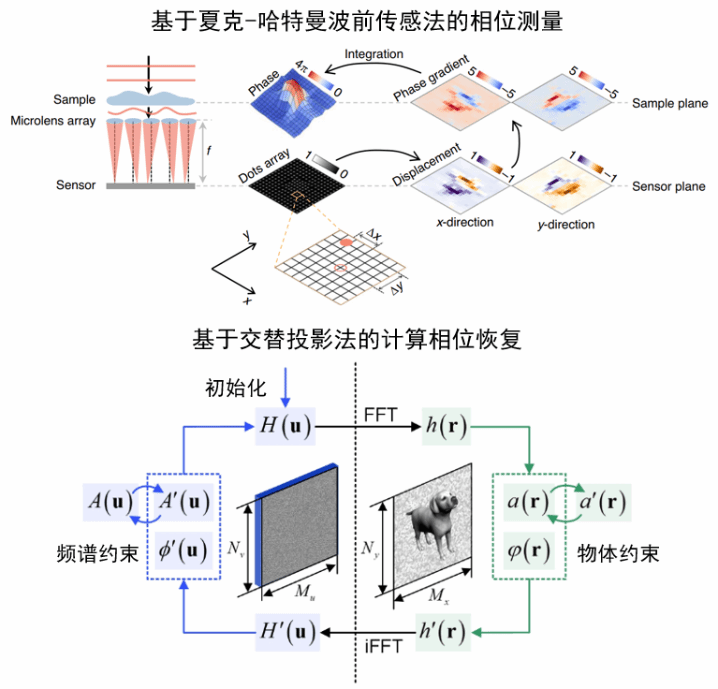
图 相位测量与计算相位恢复

现在，当别人问你计算光学成像是什么这个问题时，你是不是知道该怎么回答了？

世界的进步不会因为一个人或者几个人甚至很多人的固执而停止下来，认知的维度决定了你的高度。当你觉得无路可走的时候，该考虑一下是不是困在了低维的空间中。