从波前、自适应光学到计算成像的数学表示|邵晓鹏专栏第三季

最复杂的问题是简单化，最简单的问题是复杂化。——莫名

引子

这几天，X卫星公司的杨总摊上事了，用他的话说：上吊的心都有了。这几年，公司发展不错，接了很多航天项目，从一个不见经传的草台班子变成了行业内冉冉升起的一颗新星，据坊间传说，公司上市那是早晚的事儿，尤其是解决这颗高分辨率相机载荷的研制，这标志性成果可以说是牛上天了。可是，麻烦就出在这里。当时为了竞标这个载荷，公司下了血本，牛吹得也大，逼得同行直呼简直无路可走，杨总呢，自从拿下这个标之后，连平时走路都觉得路很宽，经常横着走。现在的麻烦是公司尽管高薪挖了行业大佬一批，从草台班子V1.0升级到V3.14，但草台班子的质朴品质依然保持良好，导致其质量问题层出不穷，一直困扰着他们。

杨总刚挂掉甲方毫不客气的告诫电话，负责光学制造部门的老牛就急急火火地跑了过来诉苦：“杨总，这活干不成了、干不成了！你说那个小朱，那设计的叫什么玩意儿，精度高得不得了，还牛哄哄地命令我们必须要一个月加工完！更差劲的是，他的设计根本就不考虑装配工艺，那么高精度的镜子到装配环节，压根就没用。我也问总设计师老马了，他给我讲了一堆道理，但也解决不了问题。把压力都压给工程后面的环节，越是最后，压力越大，到了我们部门，几乎什么压力都传递到我这里了，我干不了这活！”嘴上一圈泡的杨总端起茶杯喝了口水，哇地一下就吐了出来，烫得嘴上的泡更显得晶莹了，然后，一挥手：“老牛，你先出去一下，我想静静……”

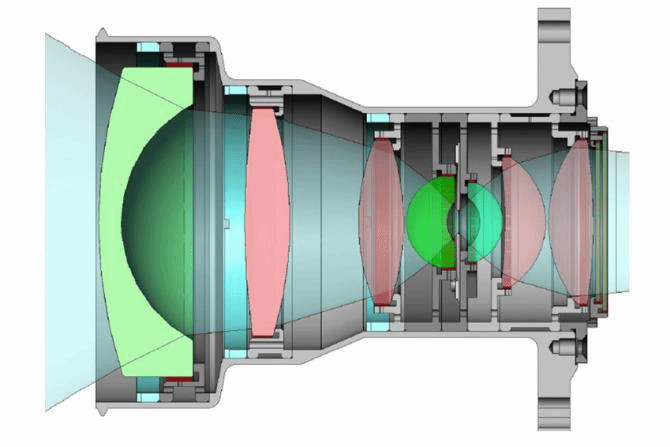
图 光学装配

老牛无奈，排解郁闷，请了一帮兄弟晚上喝酒。推杯换盏，随着酒杯见底，话也就多了起来。吐槽的有，吹牛的有，胡说八道的更有。借着酒劲，平时不太说话的，现在也话多了起来。突然，酒桌上一个新来的博士小苟过来给老牛敬酒，说听同事经常讲老牛不易、忍辱负重云云，不过，这也不是办法，最近他听过几次关于计算成像技术的报告，经常会有专家提镜子的光洁度与成像关系的问题，于是他便也思考了起来，借敬酒之机，提出如下问题：一个镜子是不是一定要磨得越光滑越好？到底要精度达到多少分之一波长才可以应用？多片镜子装配完之后的整个光学系统，它的精度要达到多少？如果有大气、水等介质干扰的情况下，光学系统的整个波前已发生了很大变化，它的精度下降严重，成像质量可想而知，那问题是我们还有没有必要费劲把镜子加工那么精细？

图 光学表面抛光

老牛说：“小苟，你说的都对，我也听过那个叫啥的教授来公司讲过计算成像，成天道理一大堆，尽吹牛！他还写会议、办科普、卖书，搞得还洋火不行。他送给杨总一本签了名的书，老杨顺手就给了我，让我学习学习。我一个负责光学制造装配的，喝不惯那像极了洗脚水泡出来的‘猫屎咖啡’，标价158元一杯，那么贵，还好意思卖！现在呢，我把那本书垫在办公室花盆下面了，哎，别说，还真不错！也算是发挥它的最大价值了，哈哈哈，喝酒……”

数杯过后，老牛拍拍了小苟的肩膀，意味深长地说：“小苟啊小苟，我跟你说，计算光学在航天航空上就根本没法用。我认识的仇（准）院士就经常给我说计算成像不行，人家水平真是高，我最服气，他的话肯定没错。不信，你看看现在哪个地方不都是把镜子磨得一个比一个光，不光怎么成像啊！有大气怎么了，我们还可以上自适应光学啊！”

小苟也是疑惑：到底听谁的？

人最怕的就是没有主见。缺少思考的人，满脑子只有别人的观点，却没有自己的想法。理性的回答应该是听自己的，遵循自己的内心，当然，自己要有充分的知识储备，理性思考。

光电成像的核心问题实际上就是对抗像差的过程，当然，严格地讲，应该是波前的问题。那我们就来看看波前到底是个啥，它与成像到底有何关系？

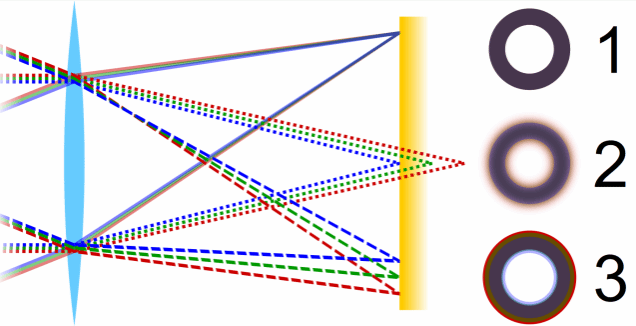
图 光学像差

一、波前（wavefront）与像差
1、波前

实话说，波前这个词的翻译确实很不友好，看起来不像是名词，不仅感觉神秘，而且会让人望其文而生歧义，尤其是非光学专业人士。

老套路，我们来看看维基百科怎么解释波前的问题。

波阵面（英语：wave surface）简称“波面”，为波在介质中传播时，经相同时间所到达的各点所连成的直线、曲线（二维内）或面（三维内）。也就是说，它指的是某一时刻波动所达到的各点所连成的曲面。最前方的曲面叫做“波前”（英语：wave front），后面的波阵面亦可叫做波前。波阵面质点的振动情况与机械波的波源初始振动情况相同。由于同一波阵面上各点的振动相位相同，所以波阵面是同相面（即相位差为零）。

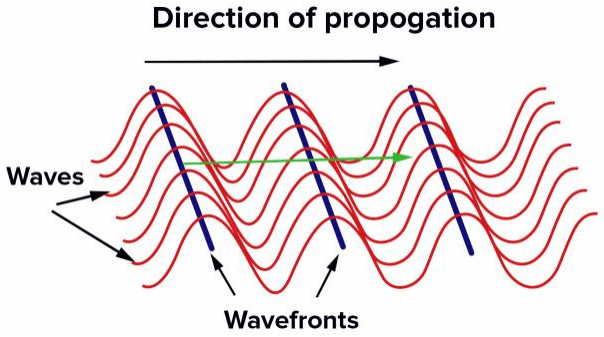
图 波前

从维基百科这寥寥数语便能看出，波前的本质还是相位！

然后，我们再来看看几种典型的波阵面的图，看看神秘的波前到底神秘在哪里，看看它与相位的关系到底如何。平面波阵面：该波阵面是由点光源发出的波在距离无限远时近似形成的等相位面，也可以由扩展光源发出的平行光束形成。平面波前在空间中各点的波矢量平行且大小相等。球面波阵面：该波阵面是由点光源发出的光波向外传播时形成的波前，呈同心球面，相位差在各球面上相同。波从点光源向外发散，所有波前的中心位于点光源处。柱面波阵面：该波阵面是由线光源（如无限长的直线形光源）发出的光波形成的波前，该波前是围绕线光源的同心圆柱面。

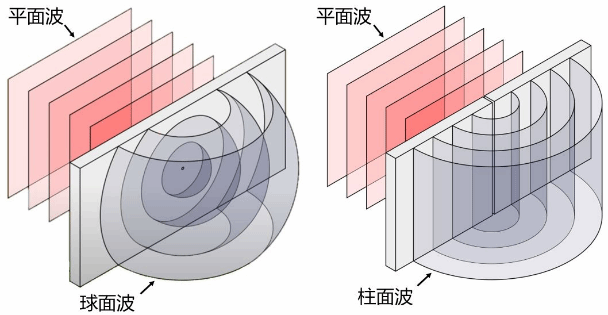
图 常见的波阵面

当光波由无限远处发射，观测范围内光线的传播方向都平行，此时为平面波，波阵面为平面。当光波由近距离发射，光线为点光源发出射线，此时为球面波，波阵面为球面。平面波经过透镜后可以变成球面波，同样，球面波经过透镜后也可变成平面波，这其实也是光学系统设计时惯用的技巧。

2、像差

像差，想必大家并不陌生。实际光学系统的成像是不完善的，光线经光学系统各表面传输会形成多种像差，使成像产生模糊、变形等缺陷。像差就是光学系统成像不完善程度的描述。在理想光学成像系统中，成像具有物像共轭关系，物点经过光学成像系统后汇聚为理想像点。而实际光学成像系统在传播过程中，由于实际光学系统都存在一定大小的视场和相对孔径，成像区域远远超出近轴光学理论的适用范围，导致实际像与理想像之间出现差异,这种差异被称为像差。此时，不同视场角和孔径高度的入射光线不再汇聚于一点。对于单色光，根据光线汇聚性质的不同，可以分为了球差、慧差、像散、场曲和畸变五种单色像差。而对于不同颜色的光，由于相同材料的折射率随波长变化，引发了位置和倍率的差异，这被称为色差。这些基于几何光学光线追迹方法得到的光线汇聚差异统称为几何像差。

图 五种单色像差和色差

对于几何像差，由于光学系统像差与结构参数之间具有确定的函数关系。以球差为例，球差是一种由于光线宽度引起轴上像差，对于目标点发出的不同入射高度h的光线在像方光轴上的汇聚位置不同，这种距离差异为球差，用δL´ 表示：

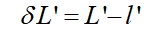
其中L´ 为边缘光线的像方截距长度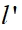，为理想成像时近轴光线的像方截距长度。球差表现为物点成像，像方不再是个亮点，而是由不同光线叠加得到的，中间亮边缘逐渐模糊的光斑，从而影响成像质量。

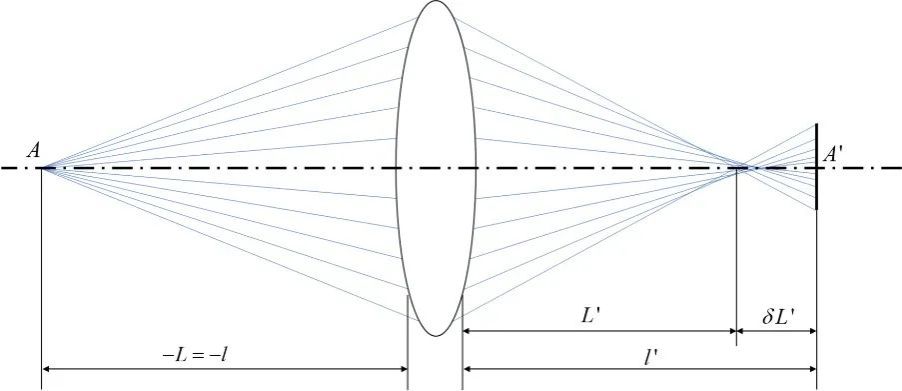
图 光学系统的球差

由于球差是关于光线入射高度h的函数，可以通过幂级数对球差进行展开，由于轴对称性，不存在奇数阶的项。球差可以表示为：

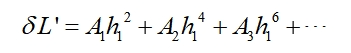
对于展开式中第一项为初级球差，第二项为二级球差，第三项为三级球差。二级以上的球差为高级球差。

根据几何像差解析式可以将解析式中的第一项称为初级像差，二级以上的称为高级像差。对于结构简单的光学系统的像差矫正工作，因为像差主要由初级像差构成，因此可通过矫正初级像差可以获得较好的成像质量。对于复杂的光学系统结构，像差尤其是高阶像差与结构参数关系十分复杂，难以通过解析表示。

另一种根据波动光学理论推导出像差理论，点目标发出的球面波通过理想的光学系统后，依然保持为球面波。然而，由于衍射效应，物点最终汇聚成一个弥散斑，而非理想的点。在实际的光学系统中，光波在传输过程中受到多种因素影响，透过光学系统后的波面不再是理想的球面波，实际波面与理想球面波之间的差异被称为波像差。

图 理想波前与受像差影响的波前

采用波像差来描述实际成像系统与理想成像系统波面的差异时,可以使用Zernike多项式可以把波前像差分解为多阶成分。由于几何像差与Zernike多项式均采用圆域极坐标描述，每一级的几何像差可以与Zernike多项式中各项对应。常用的Zernike多项式为7阶35项。0~2阶为低阶像差，3阶及以上为高阶像差。通常，高阶像差对视觉质量的影响较小，但随着光学系统口径增大、成像精度提升，高阶像差对成像质量的影响因素至关重要。

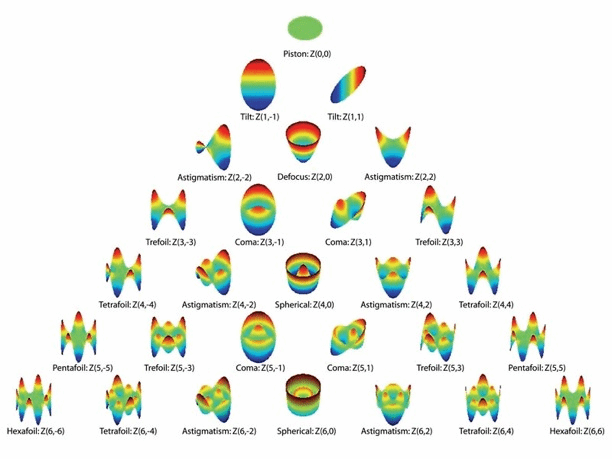
图 波像差与Zernike多项式

低阶像差是指由较简单的光学畸变引起的像差，主要为1、2阶基础像差，包括光波的倾斜、成像系统中的离焦、一阶像散等问题。这些问题通常可以通过常见的光学矫正方法解决，比如加入传统的光学镜片对低阶像差进行补偿。相较于低阶像差，高阶像差的补偿通常更加复杂，无法简单地通过加入光学镜片实现。常见的用于校正高阶像差的方法包括：复合透镜组设计、波前传感与校正、计算后处理等等，同时也可以通过自由曲面设计或者衍射光学元件实现。

二、泽尼克（Zernike）多项式

泽尼克多项式是荷兰格罗宁根大学Frits Zernike于1934年在研究相衬显微方法时提出的一组定义在单位圆上的正交多项式，由于数学性质简洁优美且和光学像差紧密联系，泽尼克多项式在提出后逐渐引起了人们的关注，被广泛应用于光学和图像处理中。1954年，加拿大阿尔伯塔大学A.B. Bhatia和美国罗切斯特大学E. Wolf进行了关于泽尼克多项式的研究，他们基于正交性和不变性等数学性质推导和研究了泽尼克多项式的性质。1981年，查尔斯·斯塔克·德雷珀实验室的Mahajan等人提出了Zernike环形多项式。在圆形光瞳基础上，将泽尼克多项式扩展到环形光瞳（即带有中心遮挡的光瞳），用于研究具有部分遮挡的光学系统的像差。这一扩展在天文望远镜和其他含有遮挡元件的光学系统中有重要应用。

随后，Frits Zernike的学生Bernard Nijboer将对称光学系统的像差函数展开为一系列泽尼克多项式，这为光学系统的衍射积分和点扩散函数提供了有效的表示方法，建立了点物体在像平面上的振幅分布。然而，该理论主要适用于小像差的情况，并且只能精确计算焦平面位置处的点扩散函数。对于大像差或非焦平面位置，该理论的适用性受到一定限制。泽尼克多项式由一组正交于单位圆上的基函数组成。这些基函数可以用来将波前像差分解为不同的成分，每个泽尼克多项式代表了特定的波前形状，例如球面形状、棱柱状等。泽尼克多项式的正交性允许将复杂的波前像差表示为一系列正交基函数的线性组合，从而便于对波前像差进行量化分析和校正。泽尼克多项式广泛用于表示各种像差，包括球面像差、彗差、像散等。标准泽尼克多项式与对应的Seidel像差类型如下表。

20世纪70年代，随着自适应光学的兴起，欧洲航天局的J. Noll提出了使用泽尼克多项式来进行大气湍流引起的波前像差的统计分析，并给出了不同阶泽尼克多项式在湍流下的贡献和方差关系。在光学系统检测与设计的应用中，广泛采用泽尼克多项式对系统的波前像差和光学表面形状进行拟合，利用泽尼克多项式对光线追迹获得的采样数据来拟合波前。亚利桑那大学的Loomis在开发的干涉图处理软件FRINGE中引入了泽尼克多项式的重排序子集，用于干涉测量中的波前分析，从而提高了干涉数据处理的效率。1980年，美国空军武器实验室Teague将泽尼克多项式的应用从光学扩展到图像处理领域，并开创了Zernike矩。该矩具有重要的旋转不变性，使其成为模式识别中的有效形状描述符。近年来，随着泽尼克多项式在各个领域的应用逐渐成熟，美国国家标准协会（ANSI）和国际标准化组织（ISO）对Zernike表示方法进行了标准化，促进了其在光学、图像处理和其他工程领域中的广泛使用。

泽尼克多项式在光学设计、光学检测、自适应光学及图像分析等多个领域都有实际应用。泽尼克多项式与其他多项式序列相比具有明显的优势。具有独立性和正交性的性质，可以添加任意数量的额外项，而不会影响已经计算的项。然而，在非圆形光瞳的光学系统中，泽尼克多项式在整个光瞳区域内不再具有正交性，这可能会对波前拟合的结果产生影响。因此，在这些情况下，通常需要采用经过修正的多项式或其他拟合方法来保持精度。

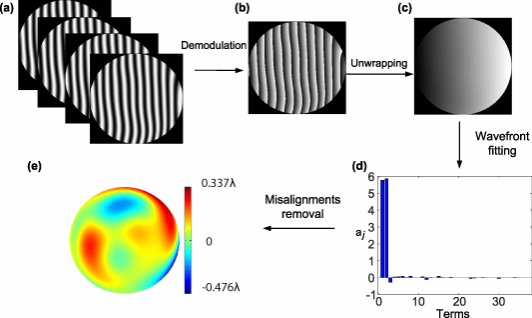
图 Zernike分解用于描述光学检测中的像差问题

三、自适应光学

大气湍流对天文观测的干扰是自适应光学技术研究的起源。1953年，美国海尔天文台的Babcock首次提出了通过一定的手段实时测量大气湍流引起的光学畸变，并通过可变形反射镜反方向补偿畸变，从而消除大气湍流对光学系统干扰的思想。1964年美国海军研究实验室M.I.Skolnik和D.D.King提出了相位共轭原理和波前补偿原理。1971年美国亚利桑那大学的R.V.Shack改进测量几何像差的经典Hartmann方法，研制了Hartmann-Shack波前传感器，由于其稳定性好、精度高，目前已成为现代自适应光学中被广泛采用的波前传感器。

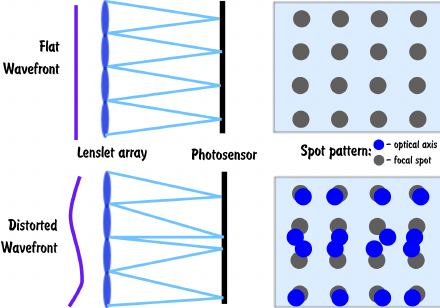
图 Hartmann-Shack波前传感

20世纪80年代末，人们开展了自适应光学在天文观测方面的应用研究。欧洲南方天文台（European Southern Observatory，ESO）联合法国空间研究院和Laserdot公司（今法国CILAS 公司的前身）开展了名为Come-On的自适应光学研究计划，其成果于1989年被安装在法国Haute Provence天文台的1.52 m望远镜上，在2.2 μm以上波段的成像结果接近衍射极限。该系统被安装在位于智利La Sila的欧洲南方天文台3.6 m望远镜上，使其探测极限达到11.5星等。日本国立天文台的Subaru望远镜口径8.2 m，采用CILAS公司研制的188单元双压电片变形镜校正像差，并采用曲率波前传感器测量高阶波前畸变。其优势是双压电片变形镜可以在局部产生近似球面的面形，可直接根据曲率波前传感器每个子孔径的测量结果直接驱动变形镜，无需波前重构环节。

图 Subaru望远镜

虽然，近几年自适应光学的发展非常迅速，并广泛应用于天文观测领域，但是依然存在一些技术难点亟待探索。

第一是波前探测的灵敏度。由于大气湍流的时变性特点，波前传感器需要非常高的时间分辨率来捕捉波前畸变。光信号在通过大气湍流时可能会出现信号衰减，尤其在低照度条件下，探测信号较弱，因此需要波前探测器具有高灵敏度，以保证其工作性能；第二是强大气湍流下的高精度波前探测。目前，波前传感器主要针对大气湍流所引入的光学像差，其特点在相位连续，因此能够通过直接积分的方式准确获得波前信息。然而，在强湍流条件下，会出现相位非连续的相位奇点。由于相位非连续，直接积分的方式无法准确获得这些相位奇点信息，从而使得强大气湍流环境下的波前校正效率降低；第三是波前校正视场受限。由于大气湍流具有随机性，因此波前校正存在等晕角限制，即：在空间某一位置测得的波前信息，仅在有限范围内有效，因此极大地限制了波前校正的视场。

Multi-Conjugate Adaptive Optics（MCAO）是目前解决视场问题的主要方式之一，该方法通过使用多个变形镜以及波前传感器同时测量并校正大气湍流中不同层面上的像差，以增大视场范围。但是，探索更加高效的大视场波前校正方案依然紧迫。

与此同时，随着相机性能以及计算机算力的大幅提升，自适应光学数字化也是未来发展的重要趋势。传统的自适应光学技术采用变形镜构建共轭相位补偿波前像差，而自适应光学数字化采用计算方式自适应补偿成像过程中波前像差，通过计算成像代替相差补偿结构，在复杂场景中对光场的强度、相位、偏振、光谱多维度进行测量与计算，根据目标特性重新分配光场信息，降低环境干扰，实现目标的分离与提取。不同于传统机械自适应光学技术，自适应光学数字化研究传输介质对波前相位的畸变与复杂光场信息传输，通过引入新体制成像模型、高性能以及智能化算法设计，实现高效率数字化波前校正，完成全光场信息的探测与复原，同时能够进一步压缩系统体积、降低设计成本、增强波前校正灵活性。

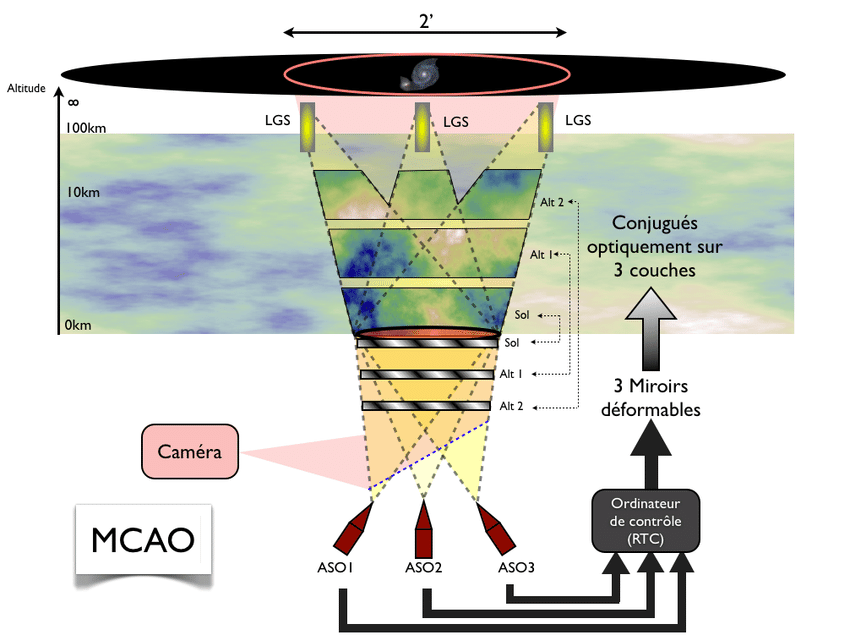
图 Multi-Conjugate Adaptive Optics（MCAO）原理

四、成像该怎么表示？

如果把光学成像的过程认为是如何用光“绘制”出物体之影像的话，那么，最直接的办法就是物像共轭，小孔和透镜都能干这事，其本质是用光的强度来干活的；但要成出来更好像质的像，那么代价就要大很多，消像差成了家常便饭；而即使消除了像差，当大气扰动等干扰进来后，又不得不呼唤自适应光学。间接的方式其实就是计算成像，即记录光场信息，从多维度光场中重建出符合人眼视觉的强度分布图，它与直接方法最大的不同是干活的主角是光场，像差已经变成了光场一个维度的描述问题，而这个描述其实就是相位场。

换句话来说，对于成像而言，只需要知道强度分布场和相位分布场的信息，理论上就可以完整地表示成像结果，只是这个结果还不够彻底，需要一个非线性的数字化重建，其过程宛如自适应光学中根据已知波前控制变形镜一般，通过数字计算过程让相位场的各项值趋近于0，此时，光强场最终会由模糊、畸变变成清晰的图像，而这个图像恰恰可以比拟传统光学中穷尽各种光学系统设计方法设计出一枚镜头、不惜代价上自适应光学，最终得到接近于光学衍射极限的结果。

这其实是我费了九牛二虎之力讲像差、讲波前、讲自适应光学，穷尽所能地把它们统一到相位这一个物理量，然后把成像从只有强度分布的实数场描述，升维拓展到了强度和相位的二元复数场描述，在数学表示上对成像做了一次革命。

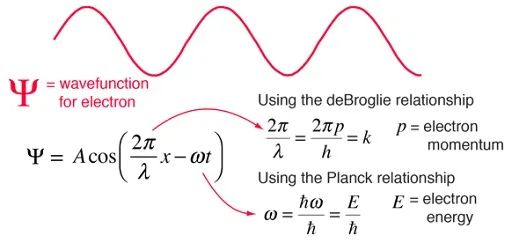
我们之前看到成像的数学表示形式都是Ax=b这种类型的，当然了，大家更熟悉的是g=f*h+n这种形式，它的本质是线性模型，其局限性我已在很多篇文章里写过。这种表示还有一个问题就是模型中所有的数都是实数，而到了有像差、有波前畸变等情况下，光场变成了复数场，也就是有了相位场，消像差、自适应光学等处理过程本质上其实就是在想尽一切办法消除相位差，或者说是让相位差归零或趋近于零，这也就是物理上的那个共相。如果我们把消像差和自适应光学的过程数字化表示之后，显然，原先需要在光学上施加的物理过程就可以用数学的方式来解决，此时的代价就比物理上要小得多了。但，这个过程说起来简单，做起来却非常复杂，面临的主要问题是两个规模不一样的矩阵做数字化“共相”的非线性处理，其难度绝非逆卷积之类处理那么简单，而这个过程恰恰又是最关键的，需要从根子上解决问题，因为，我们必须得从物理上把这事儿解释清楚。

五、挺进无人区

在物理上，共相的难度很大，自适应光学如此，对合成孔径来讲，更是难上加难。科学家们很早就想着如何把物理的共相过程变成算法过程，也就是把物理上的共相问题转换到信息域解决，由物理上的变形镜、液晶调制等实现的相位调制方法变成了纯粹的数学问题，但到目前为止，因为其物理过程过于复杂，尤其是到信息域如何处理，依然还只是一种设想，于是，它就成了一片无人涉足的无人区。

图 欧洲南方天文台超大望远镜干涉仪

无人区里有宝藏，挖宝需要光学、信息和数学方面的各路英豪全力配合，一起努力，才有可能找到宝藏的钥匙。

挺近无人区，首先面临的是相位（波前）感知探测的问题，因为目前还没有一款探测器能解决能量和波前的同时探测，而且波前感知本身就比较复杂，使用导星的主动探测方式对成像来讲应用范围将受到很大的限制，而被动波前感知方法尚不成熟，这可以说是需要解决的最关键一步。当然，这也是最受人质疑的一点。

图 直接波前探测方法

然后面临的问题是复杂的数学模型，尤其是非线性问题，对于习惯于点扩散函数的处理者而言，将是一个巨大的挑战，因为一不小心就很容易习惯性地掉入线性处理的思维大坑中，我跟很多人讨论问题时就发现，他们很难改变线性的思维惯性，在这个步骤中，绝对不可以！接下来，我们面临的问题就是数字计算的问题，尤其是会涉及到大量低信噪比的处理问题，传统的数字信号处理很难奏效。在之前的文章中，我多次讲过AI的介入，对解决这个问题会很有帮助。

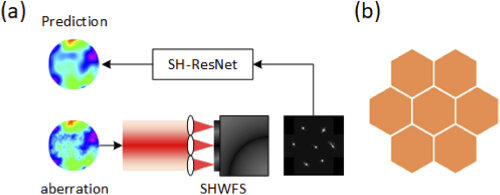
图 基于深度学习进行波前探测

米开朗基罗说：“我在大理石中看到了被禁锢的天使，只有一直雕刻，才能将他释放。”来，把油加上，铆足劲，让我们一起挺进无人区！